类C-HGB开始的高超声速滑翔器的机动能力(Maneuverability of HGV from semi C-HGB)

Previous C-HGB article was mostly aboua simple glide ballistics but still haven’t talked about the maneuverability of hypersonic gliders. Military nerds like to talk about how hypersonic gliders are but never really about how maneuverable they capable. This parts belongs to the additional section that simply calculates the relevant performance.

The calculation here is actually quite simple, you can calculate the turning rate by giving the acceleration and velocity. All you need to do is calculate the turning rate over time for the change in velocity and constant acceleration and integrate the curves to get the turning angle that the hypersonic glider can achieve for a given initial and terminal velocity.

Ultimately the turning angle is basically determined by the lift-to-drag ratio/initial velocity/terminal velocity of the turning maneuver. I’m going to organize this part and put it together with other stuff later.

Here’s a diagram to make it easier to understand.

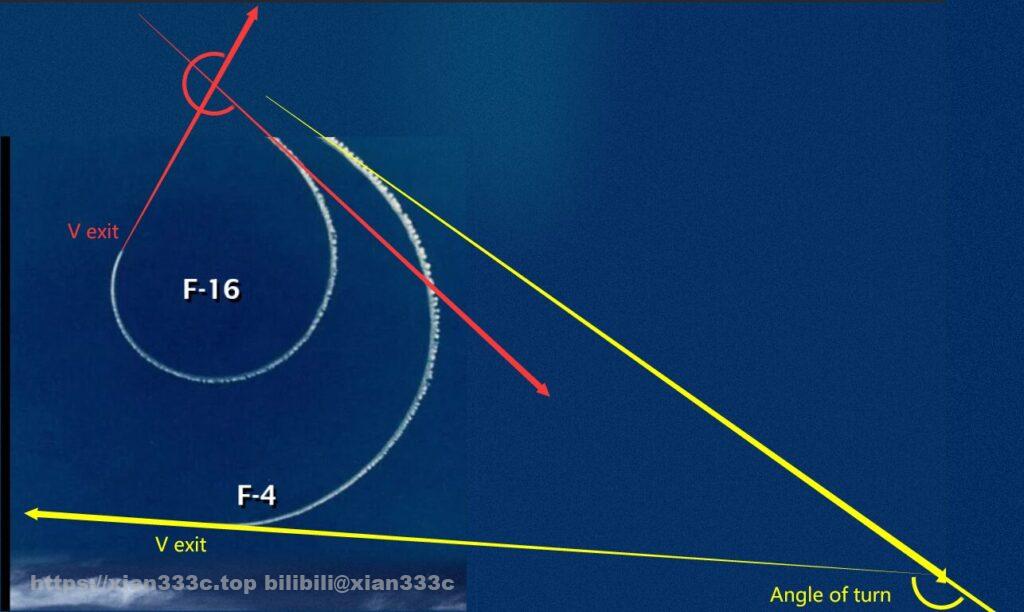
In practice, the turning angle can be calculated using the terminal velocity of the vehicle at different gliding distances as initial velocity with an expected terminal speed of maneuver and lift-to-drag ratio.

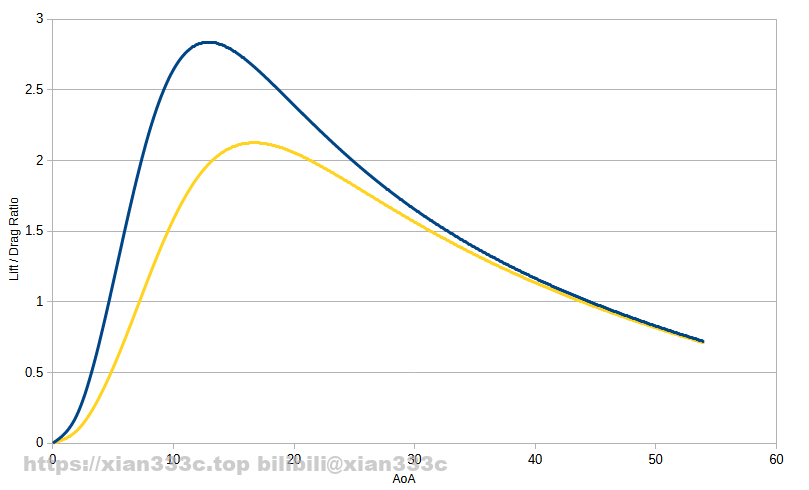
Several different values can be taken in the calculation, the maximum turning angle is achieved at the maximum lift-to-drag ratio, when the relative lift coefficient is the lowest and the turning is the slowest, which is actually the upper limit of the theoretical turning rate under the ideal.

Under the maximum lift coefficient, the lift-to-drag ratio of different vehicles are similar, here simply take the Newtonian flow as an example, and take the lift-to-drag ratio under the maximum lift coefficient. It can be taken as a constant value of 0.62. In the middle just take a fixed ratio of the maximum lift-to-drag ratio, here calculate 60% of the maximum lift-resistance ratio.

Similarly, the sustained turning rate of a fighter jet is always less than the maximum turning rate, and the same thing for a hypersonic glider. The larger the turning rate, the smaller the turning angle that can be achieved with the same energy. I’m giving here the turning angle at a local Mach 2/3 speed at the end of the maneuver.

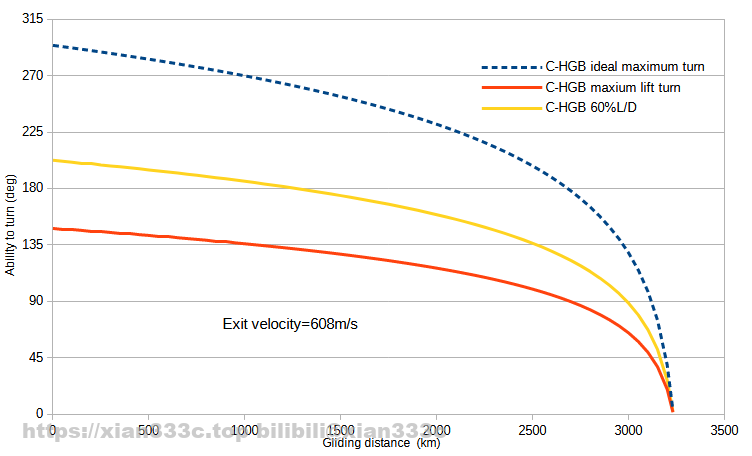
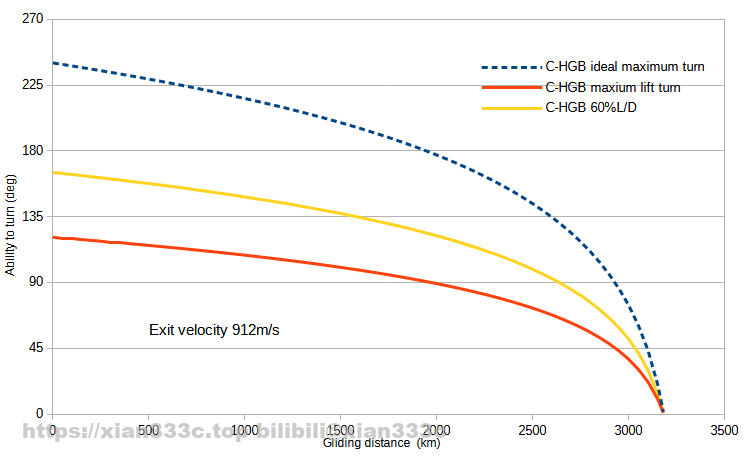
In terms of starting to maneuver at a glide distance of 3,000km, turning until speed is reduced to Mach 3, you can turn your head at about 51°. If you continue to turn till Mach 2, you will be able to turn your head by 88°.

Of course, in practice it may not be necessary to glide that far, 90° or so is a reasonable range, which is about the same as being able to do a right-angle turn maneuver, and then the speed is down to Mach 2-3 or so.

While this now tells you what the value is, what exactly does this value mean? In a simple example, the HGV is intercepted by a missile while flying towards a target, so the HGV maneuvers (turn 1). After avoiding this missile, the HGV performs a new maneuver (turn 2) and flies towards the target.

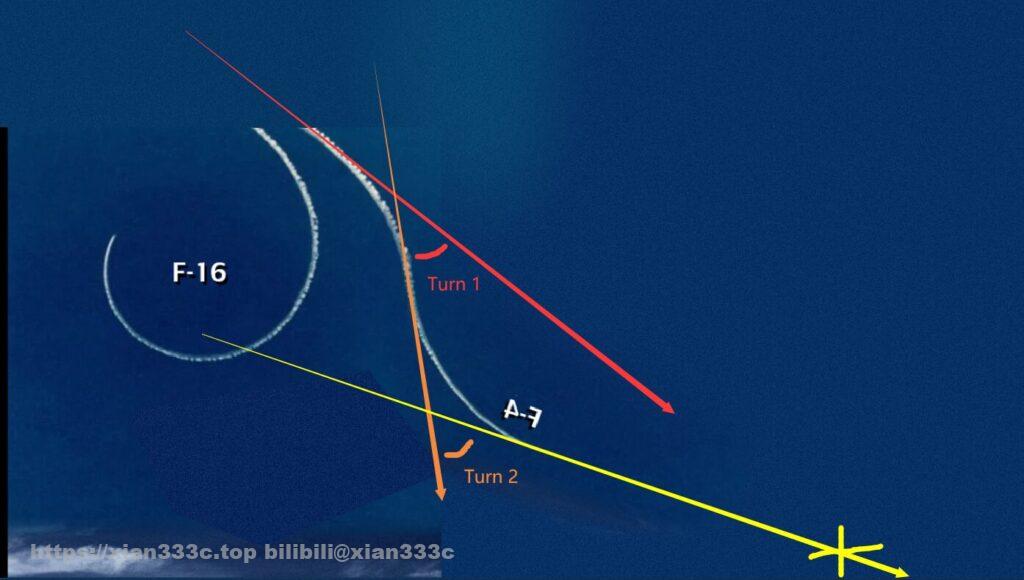
In the most ideal case, the turn occurs at an infinite distance from the target, and the original path (red) is parallel to the recovered path (yellow). And Turn 1 = Turn 2. But in reality, the target is always a finite distance away, so in practice, Turn 2 always greater than Turn 1.

So we know that as long as the first turning angle of the HGV is ≥ 1/2 the maximum turning angle, the HGV will not have enough energy to reach the target.

Taking 90° here, that’s 45°of Turn 1.

This also gets at the basic method of intercepting HGVs; even if the missile intercepting the HGV can’t hit the HGV, just multiple missiles forcing the HGV to perform multiple evasive maneuvers is enough to make the HGV lose too much energy to hit the target. On the other hand, the HGV will lose energy dramatically in the maneuvers, and eventually, the HGV’s linear velocity can easily be reduced to a level that is lower than the interceptor missiles and won’t even be much more difficult than intercepting an SR71. Of course, the actual SR71 has a much higher lift-drag ratio than the HGV still has sustained power, and wouldn’t have had to worry about being drained of energy like the HGV.