Simulation of semi LRHW/C-HGB design.(类LRWH/C-HGB高超声速弹头的仿真)

Generally, military-related technology gets dismissed as mystery magic by the internet and stupid fights with the fancy cool nouns of technology, so I’m happy to pull some of it.

I modeled and simulated some basic aerodynamic performance data for LRWH’s C-HGB hypersonic warhead this time. There were a lot of cases to run, so I couldn’t use too large a mesh for each case, otherwise, the whole simulation would have taken over a month to produce results. If I get a new workstation or server someday, I’ll probably re-run it. The fact that I simply ran through the mesh correlation doesn’t affect the results but simply makes me feel a bit uncomfortable.

Of course, I can’t guarantee that the models are the same as the original design, so there’s a more foolproof way of putting it here. Just call this a C-HGB-like warhead.

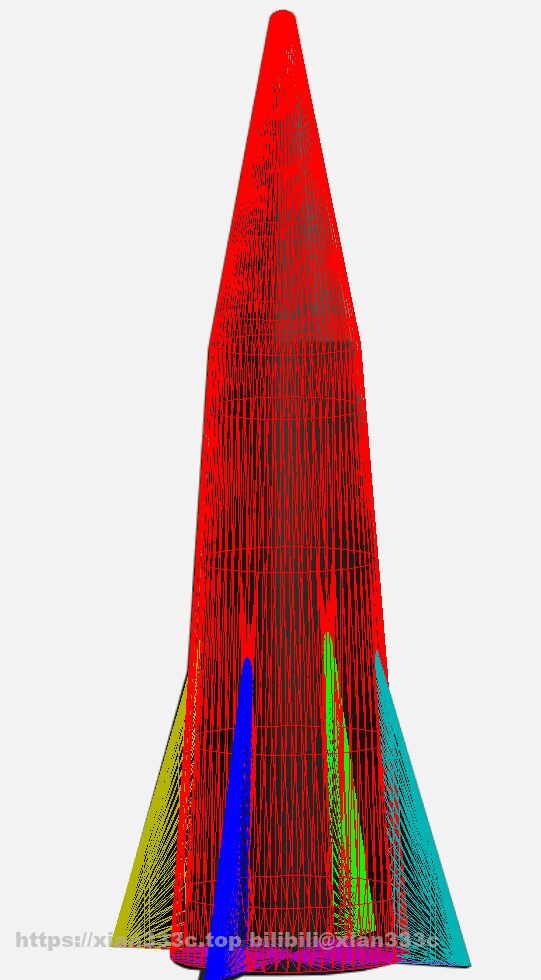
Here are some basic parameters, of course, there can be some differences between the data here and the real thing, but ultimately the important thing are a few dimensionless parameters.

• Horizontal area Sref = 0.58 m2
• Frontal area 0.1659 m2
• Horizontal area / frontal area 3.5
• Volume V = 0.13338372 m3
• V^2/3/S = 0.45
• AR = 0.893
• pressure 287.14 Pa
• temperature 250.4 k

As can be seen, the C-HGB is generally shorter and stouter as a hypersonic vehicle, due to the limited headroom of the rocket carrier considering there are submarine-launched platforms for C-HGB. This is detrimental to hypersonic flight in general. Comparatively, the C-HGB’s V^2/3/S is a bit lower than the cone warhead, due to the C-HGB’s use of a relatively large wing, which compensates for the performance to some extent.

The whole CFD came down to over 26 different cases. of course, I couldn’t show every figure so there are two.

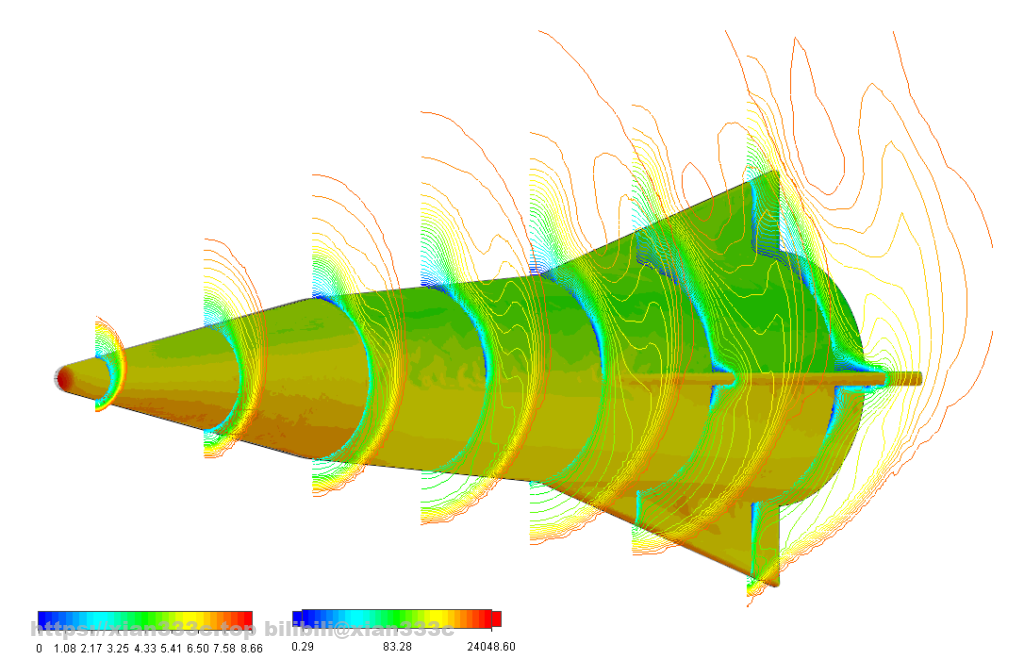
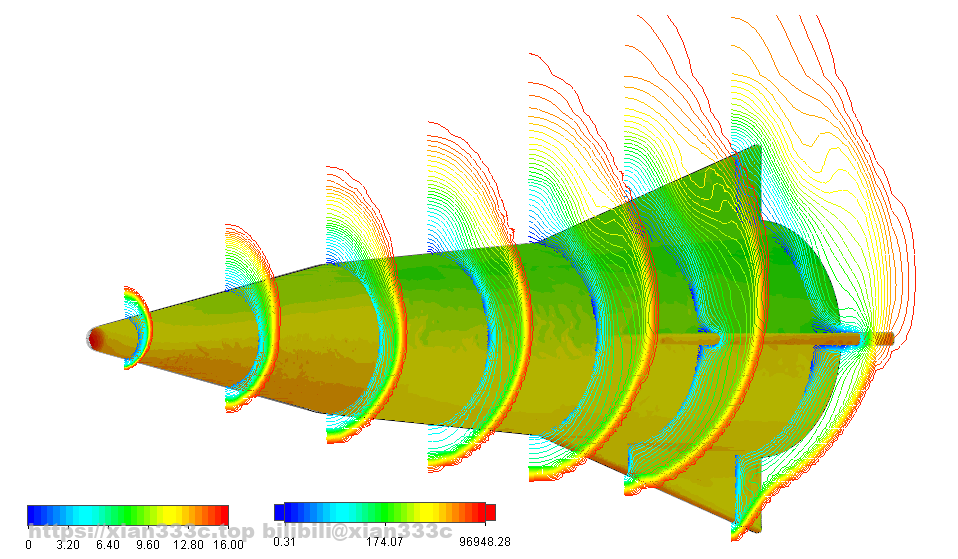
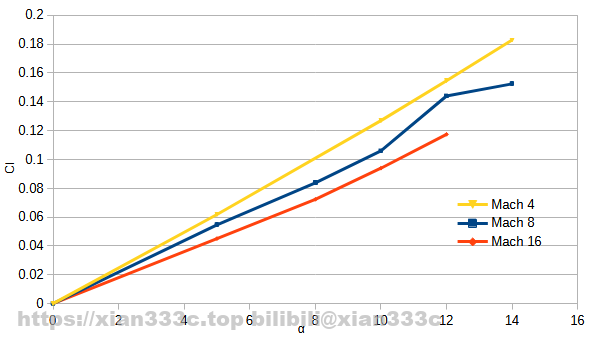
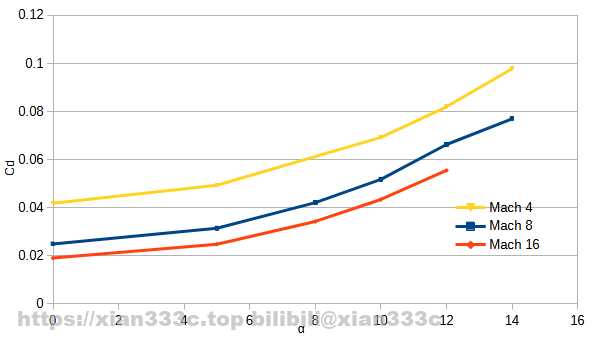
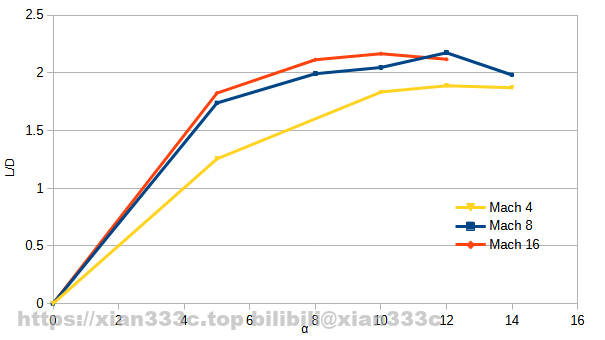
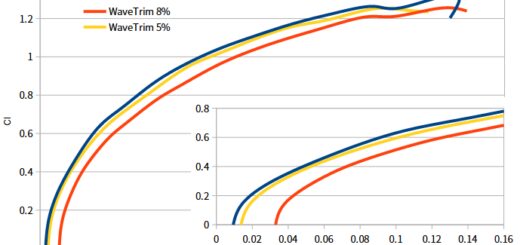
First things first, the basic lift-drag coefficient and lift-drag ratio, you can see that the overall drag coefficient of the C-HGB-like increases with decreasing Mach number. This is common to all vehicles of this Mach number, and Clα decreases as the Mach number increases. The maximum lift-to-drag ratio for the C-HGB-like is near 2.15.

In addition to the cruciform attitude, the C-HGB can also fly in an X-shaped attitude as shown. The simulation of the X-shaped attitude at Mach 8 yields a similar lift-drag performance as the cruciform.

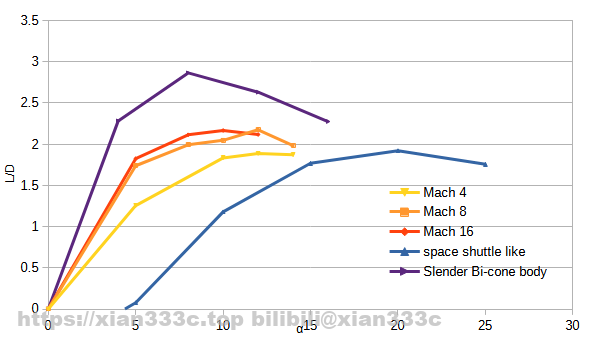
For comparison, I’ve looked up data from two other hypersonic vehicles here:

• slender bi-cone body¹: slender bi-cone body with higher lift-to-drag ratio, the original article has no more details.
• space shuttle like²: Shuttle-like hypersonic glider, hypersonic wind tunnel validation example.

A hypersonic warhead glides by slowly losing kinetic energy. Here, a simple model can be used to obtain the glide trajectory at the maximum lift-to-drag ratio which is known. The weight of the warhead is estimated to be 270kg with a density of 2.025g/cm3.

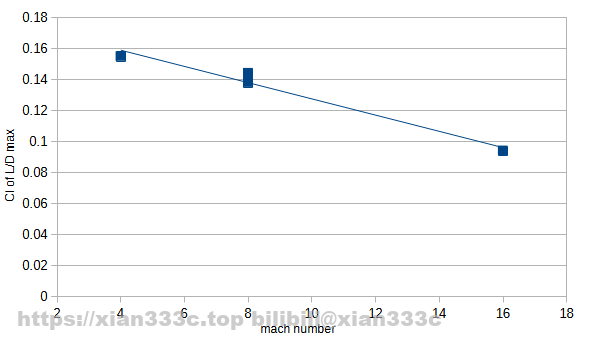
First, the lift coefficient for the maximum lift-to-drag ratio is known to vary with Mach number. Here it can be described using simple equations. The relationship between Mach number and airspeed is known

Cl = KM+a
M = V/C
Cl = K(V/C)+a

One can easily obtain the equation in gliding flight:

(KV/C + a)V2Sρ=2m

where K and a are constants describes the relationship between the lift coefficient and Mach number, V is the airspeed, C is the local sound speed, ρ is the fluid density, and m is the mass of the vehicle. The airspeed and Mach number can be plotted for different altitudes.

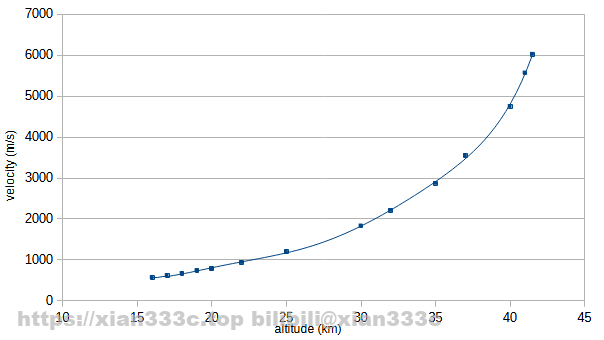
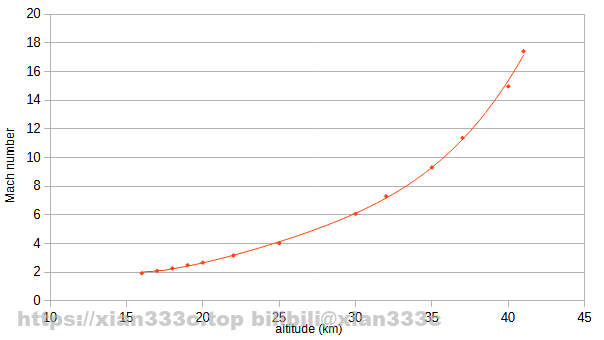
Next, the curve is interpolated, with a lift-to-drag ratio then can be plotted to show the relationship between glide distance and speed, Mach number, and the trajectory of the hypersonic glide. There is a slight difference in Mach number here because I didn’t adjust for the speed of sound at different altitudes.

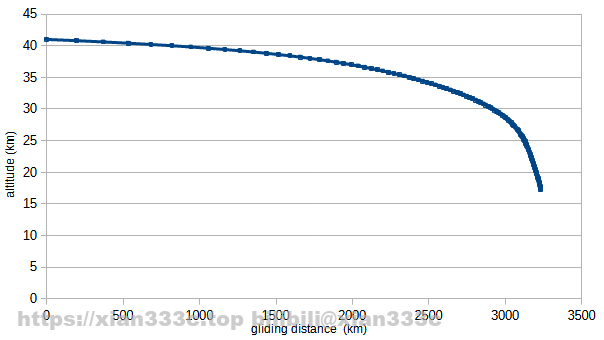
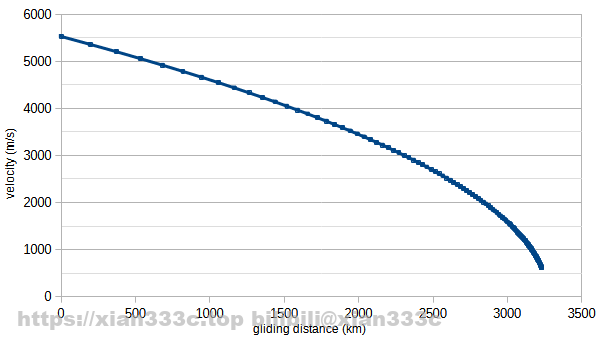
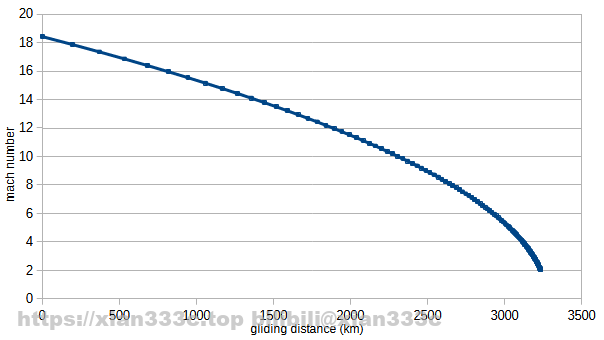
It can be seen that the gliding distance is 3200km from Mach 17³ to Mach 2 of local sound speed. For details, you can check the related information⁴.

The original paper gives the mach number refer as the sea level speed of sound, 340.3 m/s. Plot the average Mach number of gliding trajectory flight, using the sea level speed of sound as the Mach number. Find the glide distance of Mach 10 flight.

It can be seen that a Mach 10 flight speed corresponds to a gliding distance of 3095km and that the flight speed at the end of the glide is Mach 4, the sea level speed of sound.

1. 朱广生等:高超声速轴对称再入机动飞行器气动外形设计与布局研究 ↩︎
2. F. Ding et al. / Acta Astronautica 111 (2015) 178–197 Novel inlet–airframe integration methodology for hypersonic waverider vehicles ↩︎
3. https://www.twz.com/35369/army-shows-first-ever-footage-of-new-hypersonic-missile-in-flight-and-impacting ↩︎
4. U.S. Hypersonic Weapons and Alternatives ↩︎
5. 朱广生等:高超声速轴对称再入机动飞行器气动外形设计与布局研究 ↩︎
6. F. Ding et al. / Acta Astronautica 111 (2015) 178–197 Novel inlet–airframe integration methodology for hypersonic waverider vehicles ↩︎
7. https://www.twz.com/35369/army-shows-first-ever-footage-of-new-hypersonic-missile-in-flight-and-impacting ↩︎
8. U.S. Hypersonic Weapons and Alternatives ↩︎